

The Distance to the Cygnus Loop
Supernova Remnant
by Bill Blair, JHU
Version 1.0, November 2001
![]()
The Cygnus Loop supernova remnant is the expanding leftovers of a star about ten times the mass of the sun that exploded some 10,000 years ago in the direction of the constellation Cygnus the Swan (a.k.a. the Northern Cross). Because it is relatively nearby, it suffers little attenuation from foreground gas and dust and can be observed at all wavelengths. This makes it an important object for study, because most such objects are much farther away and more difficult to observe. Since many derived parameters depend on the assumed distance of the object (in some cases, distance squared or to the third power!), it is important to have an accurate distance to this prototypical object. It may surprise you to know that, until a couple of years ago, the distance assumed by almost all astronomers was incorrect by about 40%!
Caption: This image shows a ground-based wide field image of the Cygnus Loop (background) and a Hubble Space Telescope image of the tiny box at upper left as the inset. This faint gaseous filament has played a key roll in deriving an improved estimate of the distance to the Cygnus Loop. (Click on photo to see larger version.)
The Cygnus Loop is a HUGE object. The background picture above shows the nebular gaseous filaments of the Cygnus Loop extending across some 3.5 degrees of the sky (Note: the full moon is a half degree across!) The northeastern filaments are often referred to separately as the "Veil Nebula," but as you can see, this is just one portion of a much larger, roughly circular grouping of filaments that make up the entire object. The canonical distance for the Cygnus Loop, used by nearly all astronomers for the last 40 years or so, is 770 pc. (1 pc = 1 parcsec = 3.26 light-years. So 770 pc = 2510 ly.)
The inset in the picture above shows a lovely ribbon of light which is coming from a tiny region in the box at upper left in the figure. This filament of gas was imaged by the Hubble Space Telescope in 1998, and is at the very outer edge of the supernova remnant where the shock wave from the explosion is first encountering the surrounding interstellar gas. This image is interpretted as a gently rolling "sheet" of gas that is seen almost exactly edge-on. Slight differences in the density of the pre-shock gas causes the observed rippling effect. Here is a black and white version of the picture that shows more detail:
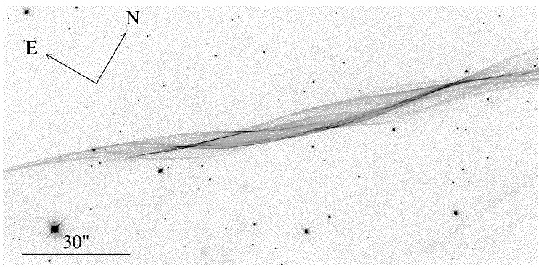
To show the situation more clearly, the picture below is provided. This picture combines two optical ground-based images (red and green) with data from and X-ray satellite (in blue). The faint red filaments bounding the blue regions just below and left of center are the same filaments as imaged with Hubble.
Caption: This image of the northeastern region of the Cygnus Loop supernova remnant shows a combination of optical and X-ray data. Red indicates filaments emitting in the light of hydrogen, green shows regions emitting in the light of twice-ionized oxygen, and the diffuse blue glow shows X-ray emission. Various combinations of these produce other colors. For instance, green filaments with surrounding X-ray (blue) emissions produce a turquoise result. Background stars, which do not emit in X-rays, look yellow (green + red). The white region at lower right is very bright in all three colors. (PHOTO from J. Hester, J. Raymond, and W. Blair, 1994, Astrophysical Journal, Vol. 420, pg. 721.)
The red filaments show gas that glows in the light of hydrogen at 6563 Angstroms (an emission line called "H-alpha"). In 1994, a spectrum of these faint red filaments was published that showed this emission line could be fit with two components: A narrow core component representing conditions in the pre-shock gas) and a broader component. Here is a figure showing fits to this spectrum:
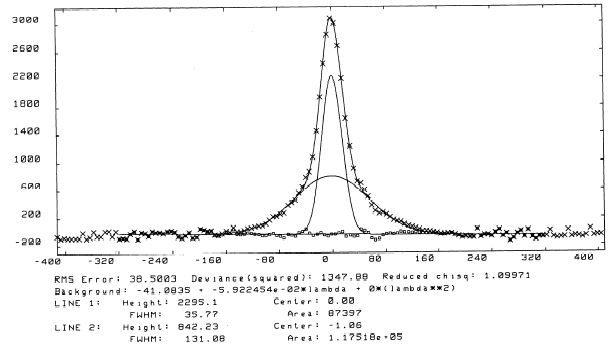
If you can see the notation about "Line 2," the "FWHM" (Full Width at Half Maximum) of the line is 131 km/s. This is a measure of how fast the gas in the post-shock region is moving. Computer models of interstellar shock waves tell us that 3/4 of the shock velocity gets "thermalized" (turned into motion of the gas), the the shock velocity at this position is 4/3 x FWHM = _______ km/s. (Note the units: kilometers per second!)
Why is this of interest to the distance of the Cygnus Loop? Well, we tend to think of objects in the night sky as being unchanging, but given enough time, we can sometimes see things move. It turns out that photographic plates of the Cygnus Loop from 1953 show our faint filament, albeit at MUCH lower resolution than the Hubble data. We did the following trick to make the comparison easier: we took our beautiful, crisp clear Hubble picture and we smeared it out with the computer so that it looked like that yucky old ground-based picture from 44 years earlier! Then we compared the position of the filament to nearby stars which had remained in the same relative positions over the same time span (and hence are probably distant background stars). Here is the comparison:
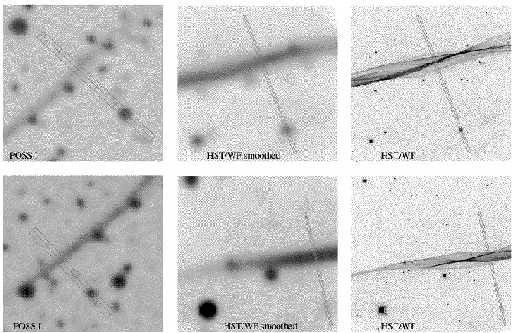
The long narrow boxes on this figure show a couple of places where we took cross-cuts that go through a star (for a reference point) and then cut across the filament. When we do this for the old data and the new data, we can see that the filament has moved! This is shown graphically below.
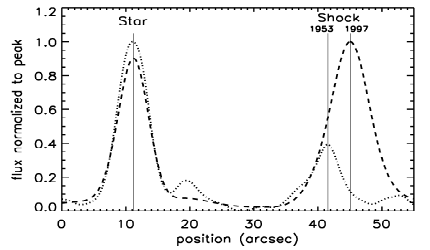
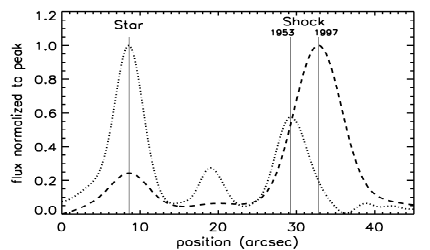
Now we're getting somewhere! By measuring the distance between the vertical lines indicating the centers of the filament at the two different times and using the scale on the x-axis of the plot, we can measure the angular motion of the filament over 44 years. We can then use some simple arithmetic and trigonometry to calculate the distance to the Cygnus Loop. Let's do it!
top panel: separation (1997-1953) = ______ mm = _______ arcseconds bottom panel: separation (1997-1953) = ______ mm = _______ arcseconds average separation: _______ arcseconds / 3600 arcsec per degree = __________ degrees. Below we will call this angle `theta'.
Next, we need to figure out how far the filament has actually moved. Since we know the velocity of the shock (units: distance per unit time) and how much time has gone by between the images, we can calculate the distance! The only other trick is converting some units:
How much time, in seconds?
time = 44 years x (3.17 x 10^7 seconds per year) = ______________ seconds.
How far has the filament moved (in kilometers)?
distance = velocity x time
= _______ km/s (from above) x _____________ seconds
= ______________ kilometers (Wow!)
Let's convert that into "parsecs":
____________ km / (3.08 x 10^13 km per parsec) = _____________ parsecs
Below we will call this distance `Y'.
Now with the distance the shock has moved (Y) and the angular change we have measured (`theta'), we can use a little trigonometry to calculate the distance TO the filament (X). In a very exaggerated form, the problem looks like this:
and the trig formula we need is just
Y Y
tan(theta) = -------- so X = -------------
X tan(theta)
If you have a calculator, this is easy! Just enter "Y" in parsecs from above and divide by tangent of theta to get the distance to the Cygnus Loop:
X = -------------------- = ____________ parsecs = (x3.26) _________ light-years.
How does this compare with the canonical value mentioned at the top of this document?
Ratio = ------------------- = ______ (x100 to get percent) = _______%.
Well here is one example. How big is the Cygnus Loop? I mentioned earlier that the angular size of the Cygnus Loop is 3.5 degrees. We can use this angle as `theta' in the "tangent" equation above, use the old and new versions of X, and calculate the diameters for the old and new distances:
Y(old) = X(old) x tan(theta) = 770 pc x tan(3.5)
= ______ pc (old diameter)
Y(new) = X(new) x tan(theta) = ______ pc x tan(3.5)
= ______ pc (new diameter)
Quite a difference, huh? If we wanted to estimate the volume swept up by the shock wave, this depends on the radius^3 (cubed), so the difference is magnified greatly. Hopefully you can see why it is important to have such a basic piece of information determined as accurately as possible!
![]()
Return to Bill Blair's Education page.
Return to Bill Blair's home page.