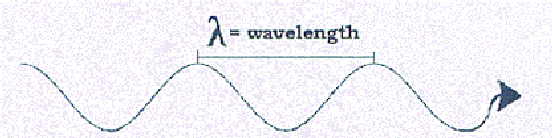The Basics of Light

The sun as it appears in X-ray light (left) and extreme ultraviolet light (right).
Light as energy
Light is remarkable. It is something we take for granted every day, but it's not
something we stop and think about very often or even try and define. Let's take
a few minutes and try and understand some things about light.
Simply stated, light is nature's way of transferring energy through space. We can
complicate it by talking about interacting electric and magnetic fields, quantum
mechanics, and all of that, but just remember--light is energy.
Light travels very rapidly, but it does have a finite velocity. In vacuum,
the speed of light is 186,282 miles per second
(or nearly 300,000 kilometers per second), which is really humming along! However,
when we start talking about the incredible distances in astronomy, the finite nature
of light's velocity becomes readily apparent. It takes about two and a half seconds,
for instance, for a radio communication travelling at the speed of light to get to
the moon and back.

Sunrise from the Space Shuttle, STS-47 mission.
You might find it interesting to remember, the next time you watch a beautiful
sunrise or sunset, that the sun itself actually dipped below the horizon eight minutes earlier--it takes
that long for the light to reach the Earth! And, of course, every newspaper article you
ever read about astronomy will always include the required statement, "A light year
is the distance light travels in one year at the speed of 186,282 miles per second,
about 6 trillion miles." (Well, 5.8 trillion miles actually, but what's 200 billion
miles among friends?)
We should also highlight right up front that light is more generally referred to as
electromagnetic radiation. Okay, we used a big word. It had to happen sooner
or later. But too often when
we say "light" it is mistaken to mean "optical light," which is roughly the radiation
visible to our eyes. Visible light is a tiny portion of a huge smorgasboard of light
called the electromagnetic spectrum. For our
convenience, we break this
smorgasboard up into different courses (appetizer, salad, etc.) and
refer to them by name, such as gamma-rays, X-rays, ultraviolet, optical, infrared,
and radio. However, it is important to remember that they are all just light.
There are no "breaks" and no hard boundaries in the electromagnetic spectrum--just
a continuous range of energy.
Particles and Waves
Physics experiments over the past hundred years or so have demonstrated that light
has a dual nature. In many instances, it is convenient to represent light as a
"particle" phenomenon, thinking of light as discrete "packets" of energy that we call
photons. Now in this way of thinking, not all photons are created equal,
at least in terms of how much energy they contain. Each photon of X-ray light
contains a lot of energy in comparison with, say, an optical or radio photon. It
is this "energy content per photon" that is one of the distinguishing characteristics
of the different ranges
of light described above. Even though it is not strictly correct, it is hard not
to think of a beam of light as a collection of little "light bullets" all strung
together in a row.
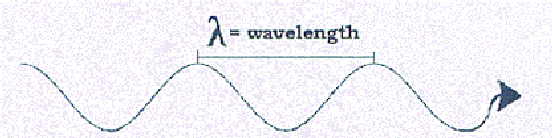
The "wave" model of light.
The other way of representing light is as a wave phenomenon. This is
somewhat more difficult for most people to understand, but perhaps an analogy
with sound waves will be useful. When you play a high note and a low note on the
piano, they both produce sound, but the main thing that is different between the
two notes is the frequency of the vibrating string producing the sound
waves--the faster the
vibration the higher the pitch of the note. If we now shift our focus to the sound
waves themselves instead of the vibrating string, we would find that the higher
pitched notes have shorter wavelengths, or distances between each
successive wave. Likewise (and restricting ourselves
to optical light for the moment), blue light and red light are both just light, but
the blue light has a higher frequency of vibration (or a shorter wavelength) than
the red light.
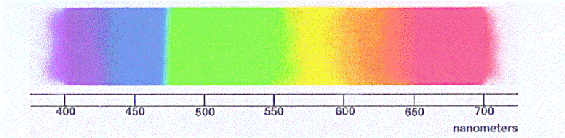
The colors of the familiar "rainbow" of visible light correspond to differing
wavelengths of the light, here shown on a nanometer scale. The wavelengths get
successively larger as one moves from left to right.
Optical light runs from about 400 to 700 nanometers.
It's the same way as we move throughout the electromagnetic spectrum. Each range
of light we have defined above corresponds to a range of frequencies (or wavelengths)
of light vibrations. These wavelengths are one of the primary indicators we use
to describe light and spectra on a graph. Displaying a spectrum as a graph instead of
just a color bar allows us to measure the light.
For instance, the "rainbow" of color shown in the figure above is what you see when
you pass white light through a prism. What may not be obvious, however, is that the
"intensity" or brightness of the light is also changing along with the colors. If
we converted the "rainbow" into a graph of light intensity versus wavelength, it would
look like this:
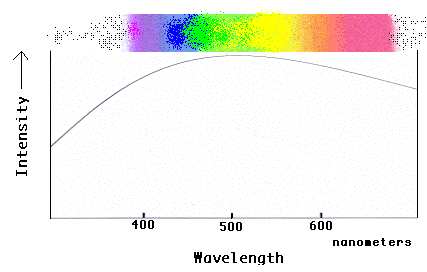
The familiar "rainbow" of the visible spectrum can be converted into a graph that
shows how the intensity of the light changes along the spectrum.
Notice that the spectrum is brightest in the middle (yellow-green region) and drops
off in both directions (toward red and blue). This was not obvious from the rainbow
version of the spectrum! Also notice that the "intensity" of the light in the
graph does not stop at the "ends" of the rainbow spectrum that is visible to our eyes!
The light continues beyond what we can see in both directions, which we can see in the
graph but not by looking at the rainbow. Astronomers use graphical spectra most of
the time because they can get more information out of the light this way, and because they
can still plot and analyze light that is not directly visible to our eyes!
Now we mentioned that the energy of each photon of light was also a basic property.
It turns out that there is a simple relationship between the energy of a photon
and the corresponding wavelength of that photon:
E(photon) = (constant) / (wavelength).
This simple equation basically ties together the particle and wave nature of light by permitting
us to convert back and forth from wavelengths to photons and photons to their
corresponding wavelengths. This equation is also in accord with what we said
earlier...an X-ray photon has a large energy (and a small wavelength) compared with
a photon of optical light.
Interaction of Light with Matter: Absorption and Emission of Light
It should come as no surprise to you that atoms and molecules (which are simply bound
collections of two or more atoms) can absorb light (= energy!). If they didn't, you
could simply flick a light on and off, and then sit back while the photons continued
to bounce around the room! Likewise, infrared light (= heat = energy!) wouldn't do any
good in heating up your home in the winter if it didn't get absorbed by matter.
Higher energy light photons, like X-rays, tend to want to plow through more matter
before they get absorbed. (Hence, their use in medical imaging: they can pass
through your "soft" tissue, but are more readily absorbed in your bones, which are
denser.) How and why do photons get absorbed by matter?
Well, it's time to develop another conceptual device to help us understand this process.
In physics, we often find it helpful to pretend we are looking at a single atom.
Atoms are made up of protons, neutrons, and electrons, and each chemical element
has a specific number of them--that's what makes them different! Protons (and neutrons)
are more massive than electrons, and so we sometimes visualize an atom as a miniature
solar system, with the heavy particles at the center (the nucleus) and the
electrons whizzing around in specific "orbits" like planets.
(In reality, this picture is not very accurate. Electrons are not
thought to be little balls "in orbit" around a nuclear "sun." However, if you get
the idea that the electrons are only found at specific, discrete "distances" from
the nucleus, and that each allowed distance corresponds to a different "energy level"
for the electron, that would be closer to reality.)
Without delving into atomic physics and quantum mechanics too far, let us just take
the following statement for granted for now: the electrons bound to any particular
atom can only be found in certain, specific
energy levels with respect to the atom's nucleus. The hydrogen atom only
contains one proton and one electron, and is the simplest
(and most common) element in the Universe, so let's use it as an example. The figure
[TBD] shows a schematic hydrogen atom where instead of drawing the allowed
"orbits" for
the electron we draw vertically-displaced lines to represent the allowed energy levels
for the electron.
If left undisturbed, our hydrogen atom likes to bind its electron as tightly as it
can, and so we would find the electron in the lowest energy level, which is called
the "ground state." However, if our atom is immersed in a beam of light from, say,
a nearby star, sooner or later the atom will encounter a photon with an energy that is
just the right amount to jump the electron up to the next higher energy level.
Voila! The photon gets absorbed, and is "gone" from the beam of light coming
from the star! Since the absorbed photon had a specific energy, this absorption
occurs at a specific wavelength in the spectrum.
Now our hydrogen atom is in what is called an "excited" state, sort of like a kid
right before Halloween. However, as all parents know, this is not the natural state
of a child, and it's not the natural state of an atom either. If no other photons
are absorbed by the atom, the electron will eventually drop back down to the lower energy
ground state. However, the atom has to lose energy to do this, and so it releases
a photon of the same energy as the one it absorbed (albeit most likely into some
other direction from which it was absorbed). This process is called emission
because a photon of light is emitted by the atom, again at a very specific wavelength.
Of course, the atom could have absorbed another photon with just the right energy
to jump up another energy level, or even two or three or more. Likewise, after each
of these possible excitations of the atom, the electron could jump back down one
or more steps, emitting photons as it went. If a photon with a sufficiently large energy
gets absorbed, it can even cause an electron to become unbound from its nucleus,
a process that is called ionization. Our crippled hydrogen atom could
then no longer absorb or emit light until it manages
to capture a free electron back into a bound energy level.
We have been discussing one specific transition or "energy jump" in one atom, but
of course in any physical system there are many atoms. In a hydrogen gas, all of
the separate atoms could be absorbing and emitting photons corresponding to the whole
group of "allowed" transitions between the various energy levels, each of which would
absorb or emit at the specific wavelengths corresponding to the energy differences
between the energy levels. This pattern of absorptions (or emissions) is unique to
hydrogen--no other element can have the same pattern--and causes a recognizable
pattern of absorption (or emission) lines in a spectrum.
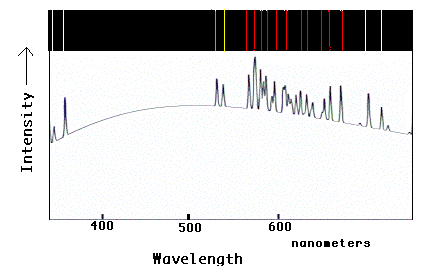
This graphic demonstrates the optical spectrum one would see from glowing neon gas,
both in colorbar and graphical formats. As with hydrogen, discussed in the text, neon
shows a specific set of spectral lines. Note how each bright colored line in the
color bar corresponds to an upward "spike" in the graphical format. Since most of the
lines are in the yellow and red regions of the optical spectrum, a neon lamp appears
"orange" to your eye. The presence of this pattern of lines in the spectrum of a glowing
cloud in space would tell astronomers that the cloud contains neon in the gas.
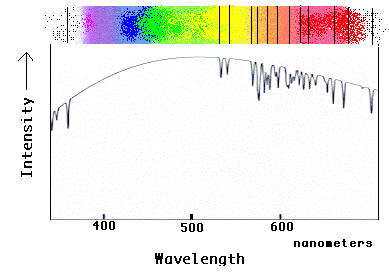
This diagram shows how the spectrum of neon would appear in the spectrum of a star.
Here, the background "rainbow" comes from the atmosphere of the star, and the neon atoms
in the star's atmosphere (or outer layers) absorb the stars light, leaving dark lines.
Note how the graph shows dips at each line position, producing the characteristic pattern
of lines expected from neon.
Extending this a bit, it should become clear that since every chemical element has
its own unique set of allowed energy levels, each element also has its own
distinctive pattern of spectral absorption (and emission) lines!
(See diagrams above for neon, for example.)
It is this spectral "fingerprint" that astronomers use
to identify the presence of the various chemical elements in astronomical
objects. Spectral lines are what allows us, from a "spectrum," to derive so
much information about the object being observed!
Click here to go to next section.
Return to Spectroscopy Home Page.
See this page in Ukranian!
Bill Blair ([email protected])